BEACON[SP'22] #

BEACON : Directed Gray-Box Fuzzing with Provable Path Pruning [SP'22]

事前知識 #

Fuzzing の分類 - 目的

Directed ~ : プログラムの特定の箇所を集中的にテスト
- 用途に関しては AFLGo を参照
Coverage-guided ~ : プログラム全体をテスト

Fuzzing の分類 - プログラムから得られる情報

Black-box ~ : 無し (+ プログラムの出力)
Gray-box ~ : 計装によるフィードバック
White-box ~ : (動的)プログラム解析 (e.g. 記号実行) による情報

概要 #

目標 #

Directed Fuzzing において:

なるべく早い段階での枝刈り
なるべく多くのパスの枝刈り
低オーバーヘッド

以上を実現するために…

目的箇所から遡り、そこに到達するための**必要条件**を求める
- 各変数に関する条件を求める
必要条件を満たさないパスを枝刈り

課題 #

既存の Directed Fuzzer での課題：

無駄なパスを大量に実行している
- 無駄なパス：目的の箇所に到達しないパス
記号実行を使っている (Savior[SP'20])
- 記号実行はスケールしない
- 充足不能な条件に時間を浪費
ヒューリスティックを使っている (AFLGo[CCS'17], Hawkeye[CCS'18])
- 目的の箇所に到達する保証が無い

提案手法 #

手法を一言で：目的箇所に到達するための事前条件を静的に求め、それを満たさないパスは早期に枝刈り

目的箇所から遡り、そこに到達するための**必要条件**を求める
- 各変数に関する条件を求める
必要条件を満たさないパスを枝刈り

→ 区間抽象化による静的解析での 2 つの最適化を提案:

Relationship Preservation (後述)
Bounded Disjunction (後述)

結果 #

Directed gray-box fuzzer : ave. 11.50x faster
Coverage-guided fuzzer : ~10.92x faster
10 new CVEs

準備 #

区間抽象化による静的解析 #

以下を順番に見る:

Data-Flow Value (DFV)
DFV の更新方法
DFV のマージ方法

Data-Flow Value (DFV) #

各変数の値を(a,b)のような形の区間で抽象化する

e.g.:

a : [20,∞)
b : [0,0]
c : (-∞,∞)

DFV の更新方法 #

更新方法は 2 つ:

代入命令
- e.g. x = 10; → x : $[10,10]$
条件分岐命令
- e.g.
```
1if (x>0)
2  ...
3else
4  ...
```
  - Then 節 → x : $[0, \infty)$
  - Else 節 → x : $(-\infty,0]$

ただし:

当該変数のみ更新
その他の変数は変更せずに伝播

DFV のマージ方法 #

マージ対象の区間全てを含む（最小の）区間を求める:

式で(ラフに)書くと:

各変数に関して、 $[a,b] \land [c,d] \rightarrow [\mathrm{mix}(a,c),\mathrm{max}(b,d)]$

精度が落ちる場合がある:

上の 3. の場合: $[20,30]$ は精度低下の原因

具体例 #

例: (順方向)

1int a, b, c;
2a = input();
3if (a > 0) {
4  b = 10;
5} else {
6  b = 20;
7}
8c = b + 50;

各行直後でのプログラムの値

1行目

1 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$
2 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$
3 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$
4 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$
5 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$
6 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$
7 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$
8 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$

1 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$
2 行目 → a : $(-\infty, \infty)$ , b : $\phi$ , c : $\phi$
3 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$
4 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$
5 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$
6 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$
7 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$
8 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$

1 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$
2 行目 → a : $(-\infty, \infty)$ , b : $\phi$ , c : $\phi$
3 行目 → a : $(0, \infty)$ , b : $\phi$ , c : $\phi$
4 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$
5 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$
6 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$
7 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$
8 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$

1 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$
2 行目 → a : $(-\infty, \infty)$ , b : $\phi$ , c : $\phi$
3 行目 → a : $(0, \infty)$ , b : $\phi$ , c : $\phi$
4 行目 → a : $(0, \infty)$ , b : $[10,10]$ , c : $\phi$
5 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$
6 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$
7 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$
8 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$

1 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$
2 行目 → a : $(-\infty, \infty)$ , b : $\phi$ , c : $\phi$
3 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$
4 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$
5 行目 → a : $(-\infty, 0]$ , b : $\phi$ , c : $\phi$
6 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$
7 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$
8 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$

1 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$
2 行目 → a : $(-\infty, \infty)$ , b : $\phi$ , c : $\phi$
3 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$
4 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$
5 行目 → a : $(-\infty, 0]$ , b : $\phi$ , c : $\phi$
6 行目 → a : $(-\infty, 0]$ , b : $[20,20]$ , c : $\phi$
7 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$
8 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$

1 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$
2 行目 → a : $(-\infty, \infty)$ , b : $\phi$ , c : $\phi$
3 行目 → a : $(0, \infty)$ , b : $\phi$ , c : $\phi$
4 行目 → a : $(0, \infty)$ , b : $[10,10]$ , c : $\phi$
5 行目 → a : $(-\infty, 0]$ , b : $\phi$ , c : $\phi$
6 行目 → a : $(-\infty, 0]$ , b : $[20,20]$ , c : $\phi$
7 行目 → a : $(-\infty, \infty)$ , b : $[10,20]$ , c : $\phi$
8 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$

パスの合流

1 行目 → a : $\phi$ , b : $\phi$ , c : $\phi$
2 行目 → a : $(-\infty, \infty)$ , b : $\phi$ , c : $\phi$
3 行目 → a : $[0, \infty)$ , b : $\phi$ , c : $\phi$
4 行目 → a : $[0, \infty)$ , b : $[10,10]$ , c : $\phi$
5 行目 → a : $(-\infty, 0]$ , b : $\phi$ , c : $\phi$
6 行目 → a : $(-\infty, 0]$ , b : $[20,20]$ , c : $\phi$
7 行目 → a : $(-\infty, \infty)$ , b : $[10,20]$ , c : $\phi$
8 行目 → a : $(-\infty, \infty)$ , b : $[10,20]$ , c : $[60,70]$

定式化 #


DFV	`dict[変数, 区間]`
解析の方向	順方向・逆方向
伝達関数	参照
境界条件	全ての変数に関して $\phi$
パスの合流	参照, 各変数に関して $[a,b] \land [c,d] \rightarrow [\mathrm{mix}(a,c),\mathrm{max}(b,d)]$
初期化	全ての変数に関して $\phi$

以降、次を仮定する:

解析の開始: Fuzzing における目的箇所
解析の方向: 逆方向

区間抽象化における精度低下の原因 #

変数間の関係は追わないために精度が落ちる例 #

crash() に到達する条件は？ (crash() から遡る)

1int x,y,z;
2
3if (z<50);
4  if (y==x-z)
5    if (y<100)
6      crash();

Motivating Example 1

6行目

3 行目 → x : $\phi$ , y : $\phi$ , z : $\phi$
4 行目 → x : $\phi$ , y : $\phi$ , z : $\phi$
5 行目 → x : $\phi$ , y : $\phi$ , z : $\phi$

3 行目 → x : $\phi$ , y : $\phi$ , z : $\phi$
4 行目 → x : $\phi$ , y : $\phi$ , z : $\phi$
5 行目 → x : $\phi$ , y : $(-\infty, 100)$ , z : $\phi$

3 行目 → x : $\phi$ , y : $\phi$ , z : $\phi$
4 行目 → x : $\phi$ , y : $(-\infty, 100)$ , z : $\phi$
5 行目 → x : $\phi$ , y : $(-\infty, 100)$ , z : $\phi$

この時点で x, z に関する情報はないため、y==x-z の関係式は使えない

3 行目 → x : $\phi$ , y : $(-\infty, 100)$ , z : $(-\infty,50)$
4 行目 → x : $\phi$ , y : $(-\infty, 100)$ , z : $\phi$
5 行目 → x : $\phi$ , y : $(-\infty, 100)$ , z : $\phi$

Q. より正確な x の事前条件は？

マージする時に精度が落ちる例 #

crash() に到達する条件は？ (crash() から遡る)

1int x,y;
2
3if (y>0)
4  x = x - 25;
5else
6  x = -x + 5;
7if (x > 0)
8  crash();

Motivating Example 2

8行目

2 行目 → x : $\phi$ , y : $\phi$
3 行目 → x : $\phi$ , y : $\phi$
4 行目 → x : $\phi$ , y : $\phi$
5 行目 → x : $\phi$ , y : $\phi$
6 行目 → x : $\phi$ , y : $\phi$
7 行目 → x : $\phi$ , y : $\phi$
8 行目 → x : $\phi$ , y : $\phi$

2 行目 → x : $\phi$ , y : $\phi$
3 行目 → x : $\phi$ , y : $\phi$
4 行目 → x : $\phi$ , y : $\phi$
5 行目 → x : $\phi$ , y : $\phi$
6 行目 → x : $\phi$ , y : $\phi$
7 行目 → x : $(0,\infty)$ , y : $\phi$
8 行目 → x : $\phi$ , y : $\phi$

2 行目 → x : $\phi$ , y : $\phi$
3 行目 → x : $\phi$ , y : $\phi$
4 行目 → x : $\phi$ , y : $\phi$
5 行目 → x : $\phi$ , y : $\phi$
6 行目 → x : $(-\infty, 5)$ , y : $\phi$
7 行目 → x : $(0,\infty)$ , y : $\phi$
8 行目 → x : $\phi$ , y : $\phi$

2 行目 → x : $\phi$ , y : $\phi$
3 行目 → x : $\phi$ , y : $\phi$
4 行目 → x : $\phi$ , y : $\phi$
5 行目 → x : $(-\infty, 5)$ , y : $(-\infty, 0]$
6 行目 → x : $(-\infty, 5)$ , y : $\phi$
7 行目 → x : $(0,\infty)$ , y : $\phi$
8 行目 → x : $\phi$ , y : $\phi$

2 行目 → x : $\phi$ , y : $\phi$
3 行目 → x : $\phi$ , y : $\phi$
4 行目 → x : $(25,\infty)$ , y : $\phi$
5 行目 → x : $\phi$ , y : $\phi$
6 行目 → x : $\phi$ , y : $\phi$
7 行目 → x : $(0,\infty)$ , y : $\phi$
8 行目 → x : $\phi$ , y : $\phi$

2 行目 → x : $\phi$ , y : $\phi$
3 行目 → x : $(25,\infty)$ , y : $(0,\infty)$
4 行目 → x : $(25,\infty)$ , y : $\phi$
5 行目 → x : $\phi$ , y : $\phi$
6 行目 → x : $\phi$ , y : $\phi$
7 行目 → x : $(0,\infty)$ , y : $\phi$
8 行目 → x : $\phi$ , y : $\phi$

2 行目 → x : $(-\infty,\infty)$ , y : $(-\infty,\infty)$
3 行目 → x : $(25,\infty)$ , y : $(0,\infty)$
4 行目 → x : $(25,\infty)$ , y : $\phi$
5 行目 → x : $\phi$ , y : $\phi$
6 行目 → x : $\phi$ , y : $\phi$
7 行目 → x : $(0,\infty)$ , y : $\phi$
8 行目 → x : $\phi$ , y : $\phi$

Q. より正確な x の事前条件は？

BEACON の手法 #

事前条件の計算 #

Fuzzing までの流れ:
区間抽象化による事前条件の計算 w/ 最適化
計装 : 事前条件を満たさない場合、枝刈り
CFG 上での Reachability 解析
分岐箇所に計装
計装済みバイナリを用いて fuzzing (省略)

区間抽象化による静的解析での最適化を提案:

Relationship Preservation
Bounded Disjunction

最適化 1. Relationship Preservation #

変数間の関係式を追跡し精度向上

手順:

変数間の演算 (e.g. y==x-z) は別で記憶しておく
- x→(-∞,∞), y→(a,b) と仮定
(伝播させる)
演算結果の変数 (e.g. z) に対する制約が判明 → 式 (e.g. x-z) の制約にする
式の制約から、演算元の変数 (e.g. x) の制約を導出する

Motivating Example 1 を用いた具体例:

1int x,y,z;
2
3if (z<50);
4  if (y==x-z)
5    if (y<100)
6      crash();

Motivating Example 1

6行目

3 行目 → x : $\phi$ , y : $\phi$ , z : $\phi$
4 行目 → x : $\phi$ , y : $\phi$ , z : $\phi$
5 行目 → x : $\phi$ , y : $\phi$ , z : $\phi$

3 行目 → x : $\phi$ , y : $\phi$ , z : $\phi$
4 行目 → x : $\phi$ , y : $\phi$ , z : $\phi$
5 行目 → x : $\phi$ , y : $(-\infty, 100)$ , z : $\phi$

3 行目 → x : $\phi$ , y : $\phi$ , z : $\phi$
4 行目 → x : $\phi$ , y : $(-\infty, 100)$ , z : $\phi$
5 行目 → x : $\phi$ , y : $(-\infty, 100)$ , z : $\phi$

追跡中の関係式:

y==x-z

3-1

3 行目 → x : $\phi$ , y : $(-\infty, 100)$ , z : $(-\infty,50)$
4 行目 → x : $\phi$ , y : $(-\infty, 100)$ , z : $\phi$
5 行目 → x : $\phi$ , y : $(-\infty, 100)$ , z : $\phi$

追跡中の関係式:

y==x-z ← これを用いて x の制約を更新

3-2

3 行目 → x : $(-\infty, 150)$ , y : $(-\infty, 100)$ , z : $(-\infty,50)$
4 行目 → x : $\phi$ , y : $(-\infty, 100)$ , z : $\phi$
5 行目 → x : $\phi$ , y : $(-\infty, 100)$ , z : $\phi$

追跡中の関係式:

y==x-z ← これを用いて x の制約を更新

最適化 2. Bounded Disjunction #

複数の制約を持てるようにする、パス合流地点での精度低下を防ぐ


DFV	~~`dict[変数, 区間]`~~ → `list[dict[変数, 区間]]` ただし数には上限あり
解析の方向	逆方向
伝達関数	参照
境界条件	全ての変数に関して $\phi$
パスの合流	下を参照
初期化	全ての変数に関して $\phi$

各ポイントで複数のパスの条件を別々で持つ
- ただし、別々でもてる数には上限あり (ref. パス爆発)
そのために、以下を変更する必要がある
- DFV
- マージ方法

DFV に対する変更 #

DFV: list[dict[変数, 区間]]
- → マージによる精度の損失を回避できる
- ただし、数には上限を設ける
  - パスの数は指数的に増える → 制約数が爆発してしまう

具体例:

1int x,y;
2
3if (y>0)
4  x = x - 25;
5else
6  x = -x + 5;
7if (x > 0)
8  crash();

Motivating Example 2

8行目

2 行目 → [{x : $\phi$ , y : $\phi$ }]
3 行目 → [{x : $\phi$ , y : $\phi$ }]
4 行目 → [{x : $\phi$ , y : $\phi$ }]
5 行目 → [{x : $\phi$ , y : $\phi$ }]
6 行目 → [{x : $\phi$ , y : $\phi$ }]
7 行目 → [{x : $\phi$ , y : $\phi$ }]
8 行目 → [{x : $\phi$ , y : $\phi$ }]

2 行目 → [{x : $\phi$ , y : $\phi$ }]
3 行目 → [{x : $\phi$ , y : $\phi$ }]
4 行目 → [{x : $\phi$ , y : $\phi$ }]
5 行目 → [{x : $\phi$ , y : $\phi$ }]
6 行目 → [{x : $\phi$ , y : $\phi$ }]
7 行目 → [{x : $[0,\infty)$ , y : $\phi$ }]
8 行目 → [{x : $\phi$ , y : $\phi$ }]

2 行目 → [{x : $\phi$ , y : $\phi$ }]
3 行目 → [{x : $\phi$ , y : $\phi$ }]
4 行目 → [{x : $\phi$ , y : $\phi$ }]
5 行目 → [{x : $\phi$ , y : $\phi$ }]
6 行目 → [{x : $(-\infty, 5)$ , y : $\phi$ }]
7 行目 → [{x : $(0,\infty)$ , y : $\phi$ }]
8 行目 → [{x : $\phi$ , y : $\phi$ }]

2 行目 → [{x : $\phi$ , y : $\phi$ }]
3 行目 → [{x : $\phi$ , y : $\phi$ }]
4 行目 → [{x : $\phi$ , y : $\phi$ }]
5 行目 → [{x : $(-\infty, 5)$ , y : $(-\infty, 0]$ }]
6 行目 → [{x : $(-\infty, 5)$ , y : $\phi$ }]
7 行目 → [{x : $(0,\infty)$ , y : $\phi$ }]
8 行目 → [{x : $\phi$ , y : $\phi$ }]

2 行目 → [{x : $\phi$ , y : $\phi$ }]
3 行目 → [{x : $\phi$ , y : $\phi$ }]
4 行目 → [{x : $(25,\infty)$ , y : $\phi$ }]
5 行目 → [{x : $\phi$ , y : $\phi$ }]
6 行目 → [{x : $\phi$ , y : $\phi$ }]
7 行目 → [{x : $[0,\infty)$ , y : $\phi$ }]
8 行目 → [{x : $\phi$ , y : $\phi$ }]

2 行目 → [{x : $\phi$ , y : $\phi$ }]
3 行目 → [{x : $(25,\infty)$ , y : $(0,\infty)$ }]
4 行目 → [{x : $(25,\infty)$ , y : $\phi$ }]
5 行目 → [{x : $\phi$ , y : $\phi$ }]
6 行目 → [{x : $\phi$ , y : $\phi$ }]
7 行目 → [{x : $[0,\infty)$ , y : $\phi$ }]
8 行目 → [{x : $\phi$ , y : $\phi$ }]

2 行目 →
[{x : $(25,\infty)$ , y : $(0,\infty)$ }, {x : $(-\infty, 5)$ , y : $(-\infty, 0]$ }]
3 行目 → [{x : $(25,\infty)$ , y : $(0,\infty)$ }]
4 行目 → [{x : $(25,\infty)$ , y : $\phi$ }]
5 行目 → [{x : $\phi$ , y : $\phi$ }]
6 行目 → [{x : $\phi$ , y : $\phi$ }]
7 行目 → [{x : $[0,\infty)$ , y : $\phi$ }]
8 行目 → [{x : $\phi$ , y : $\phi$ }]

マージ方法に対する変更 #

なるべく精度が落ちないようにマージする

マージ方法:

リストの長さが上限に
- 達していない場合:
  - リストに制約を追加
- 達している場合:
  - 以下の $L$ が最小になるような制約 (dict[変数, 区間]) を見つけ、その制約にマージ
  - $L(\phi_1, \phi_2) = \sum_{v \in \phi_1 \cap \phi_2} \mathrm{min}(\mathrm{max}(0, l_2 - u_1), \mathrm{max}(0, l_1 - u_2))$
    - $v_{\phi_1} = [l_1, u_1]$
    - $v_{\phi_2} = [l_2, u_2]$

$L$ の直感的な意味
重なる領域がある → $L = 0$
重なる領域がない → $L =$ スキマの幅

具体例:

$\text{[B, C]}$ に対して $A$ を追加したい。
Q. $A$ は $B$ と $C$ のどちらにマージすべき？

事前条件に基づく計装 #

計装方法:

プログラムを SSA 形式に変換し、代入箇所に計装する。
- 変数の代入箇所で事前条件のチェック ✅
ある変数 $v_1$ が $v_2$ のみ依存している場合、 $v_1$ には計装しない。
- $v_2$ のチェックを行えば十分

具体例:

1int x,y,z;
2assert(x<150 && y<100 && z<50);
3if (z<50);
4  if (y==x-z)
5    if (y<100)
6      crash();
7...

解析結果:

3 行目 → x : $(-\infty, 150)$ , y : $(-\infty, 100)$ , z : $(-\infty,50)$

→ 1 行目直後に計装

1int x,y;
2assert(w<5 || 25<w);
3if (y>0)
4  x = x + 25;
5else
6  x = -x + 5;
7if (x > 0)
8  crash();
9...

解析結果:

2 行目 →
[{x : $(25,\infty)$ , y : $(0,\infty)$ }, {x : $(-\infty, 5)$ , y : $(-\infty, 0]$ }]

→ 1 行目直後に計装

CFG 上での Reachability 解析 #

Fuzzing までの流れ:
区間抽象化による事前条件の計算 w/ 最適化
計装 : 事前条件を満たさない場合、枝刈り
CFG 上での Reachability 解析
分岐箇所に計装
計装済みバイナリを用いて fuzzing (省略)

目的箇所に到達し得ないパスは早期に枝刈り:

1int x,y,z;
2assert(x < 150 && y < 100 && z << 50);
3if (z<50);
4  if (y==x-z)
5    if (y<100)
6      crash();
7assert(false);
8...

 1int x,y;
 2assert(w < 5 || 25 < w);
 3if (y>0)
 4  x = x + 25;
 5else
 6  x = -x + 5;
 7if (x > 0)
 8  crash();
 9assert(false);
10...

評価 #

環境: Intel Xeon E5-1620 v3 (3.50GHz, 4core), 64GB of RAM, ubuntu 16.04
実装: LLVM bitcode 上で静的解析 + 計装
Fuzzing engine: AFLGo[CCS'17] (計装済みバイナリを AFLGo で fuzzing)
比較対象:
- Directed:
  - AFLGo[CCS'17] : 入力と目的箇所との"距離"を導入。“距離"を基に入力を変化させる。
  - Hawkeye[CCS'18] : 関数の呼び出し履歴を考慮した"距離"の導入。同上。

バグを含むリアル検体

Project	Program	Version	Input format	Num. CVEs
Binutils	cxxfilt	2.26	TXT	2
	objdump	2.28	ELF	7
	objcopy	2.28	ELF	4
Libjpeg	cjpeg	2.04	JPG	1
	cjpeg	1.98	JPG	1
Ming	swftophp	0.4.7	SWF	7
	swftophp	0.4.8	SWF	10
Libxml2	xmllint	20902	XML	4
Lrzip	lrzip	0.631	ZIP	2
Libpng	pngimage	1.6.35	PNG	1
	pdftoppm	0.74	PDF	3
Libpoppler	pdftops	0.74	PDF	1
	pdfdetach	0.71	PDF	3
Libav	avaconv	12.3	AVI/AAC	5

Bounded Disjunction : 5

実験 #

Research Questions:

RQ1: 既存の fuzzing engine に比べて効率よくバグを再現できるか
RQ2: 1. 事前条件による枝刈りと 2. Reachability 解析それぞれの効果はどの程度か
RQ3: 抽象解釈における 2 つの最適化それぞれの効果はどの程度か
RQ4: Fuzzing 時のオーバーヘッドはどの程度か

実験 1: 既存の fuzzing engine とのバグ再現における比較 #

CVE が割り当てられたバグを fuzzing で再現できるか？

見方:

$T_{AFLGo}$ : AFLGo[CCS'17] でバグを再現するまでの時間
$T_{all} = T_{sa} + T_{f}$
- $T_{sa}$ : BEACON での静的解析にかかった時間
- $T_{f}$ : BEACON で計装したバイナリでバグを再現するまでの時間
$N$ : 実行回数
$F$ : 枝刈りしたパスの割合
T.O. : Time Out (>120h)

結果:

AFLGoとの比較表

Program	CVE	$T_{AFLGo}$	$T_{sa}$	$T_{f}$	$T_{all}$	$N$	$F$
ming $_{\text{4.7}}$	2016-9827	1.25h	43s	0.31h	0.32h	0.28M	80.7%
	2016-9829	T.O.	18s	5.54h	5.55h	5.25M	82.6%
	2016-9831	2.52h	16s	0.62h	0.62h	0.47M	84.3%
	2017-7578	2.43h	20s	0.29h	0.30h	0.26M	80.8%
	2017-9988	37.99h	20s	1.45h	1.46h	1.26M	72.3%
	2017-11728	T.O.	27s	11.14h	11.15h	23.70M	84.6%
	2017-11729	4.34h	27s	1.02h	1.03h	2.02M	82.0%
ming $_{\text{4.8}}$	2018-7868	T.O.	21s	1.75h	1.76 h	3.91M	85.8%
	2018-8807	10.71h	16s	1.89h	1.89h	4.42M	83.9%
	2018-8962	35.39h	20s	1.92h	1.93h	5.96M	88.8%
	2018-11095	60.29h	20s	3.13h	3.14h	6.07M	84.9%
	2018-11225	34.23h	17s	2.84h	2.84h	4.33M	91.7%
	2018-11226	37.59h	18s	3.98h	3.99h	5.25M	89.0%
	2018-20427	T.O.	21s	3.14h	3.15h	7.81M	86.2%
	2019-9114	T.O.	22s	3.53h	3.54h	7.08M	84.0%
	2019-12982	T.O.	20s	2.47h	2.48h	4.12M	82.3%
	2020-6628	T.O.	24s	3.91h	3.92h	8.76M	84.3%
lrzip	2017-8846	5.05h	61s	1.78h	1.80h	1.32M	86.4%
	2018-11496	3.01h	68s	1.17h	1.19h	0.89M	92.4%
cxxfilt	2016-4491	7.74h	2,229s	1.38h	2.00h	7.69M	95.9%
	2016-6131	5.88h	2,258s	0.84h	1.47h	3.76M	94.9%
xmllint	2017-5969	2.07h	5,381s	0.17h	1.66h	0.33M	95.1%
	2017-9047	T.O.	5,238s	16.55h	18.01h	16.46M	83.6%
	2017-9048	T.O.	7,049s	18.00h	19.96h	18.47M	85.1%
	2017-9049	TO.	5.672s	31.56h	33.14h	40.15M	95.2%
	2017-8392	T.O.	2,654s	8.42h	9.16h	1.97M	79.3%
	2017-8396	T.O.	2,909s	39.03h	39.84h	95.85M	91.2%
	2017-8397	T.O.	3,067s	83.46h	84.31h	261.2M	96.1%
objdump	2017-8398	T.O.	2,825s	40.51h	41.29h	166.3M	96.0%
	2017-14940	T.O.	3,420s	61.38h	62.33h	41.13M	86.1%
	2017-16828	T.O.	3,326s	22.24h	10.59h	4.32M	94.3%
	2018-17360	T.O.	2,950s	45.69h	46.51h	121.55M	92.6%
	2017-7303	T.O.	2,033s	20.09h	20.65h	31.75M	85.7%
objcopy	2017-8393	T.O.	2,484s	19.78h	20.47h	20.21M	90.5%
	2017-8394	T.O.	2,671s	4.46h	5.20h	4.74M	92.3%
	2017-8395	T.O.	2,608s	3.83h	4.55h	4.31M	96.9%
cjpeg	2018-14498	49.78h	93s	11.46h	11.46h	20.12M	91.2%
	2020-13790	7.34h	106s	3.98h	4.01h	19.78M	90.4%
pngimage	2018-13785	T.O.	85s	3.22h	3.23h	65.81M	91.3%
pdftoppm	2019-10872	T.O.	4,904s	102.90h	104.26h	2.98M	76.5%
	2019-10873	T.O.	5,899s	90.25h	91.89h	3.76M	69.4%
	2019-14494	T.O.	4,153s	95.35h	96.50h	3.13M	67.2%
pdftops	2019-10871	T.O.	6,593s	62.54h	64.37h	12.94M	75.2%
	2018-19058	T.O.	2,950s	73.98h	74.80h	14.60M	86.3%
pdfdetach	2018-19059	T.O.	2,686s	82.46h	83.21h	14.21M	81.1%
	2018-19060	T.O.	2,995s	92.65h	93.48h	13.76M	70.1%
	2018-11102	T.O.	14,335s	89.57h	93.55h	6.00M	53.4%
	2018-11224	T.O.	14,893s	98.20h	102.34h	7.65M	69.8%
avconv	2018-18829	T.O.	14,623s	47.97h	52.03h	3.44M	56.7%
	2019-14441	T.O.	16,600s	52.86h	57.47h	6.89M	51.3%
	2019-14443	T.O.	14,239s	95.81h	99.77h	13.49M	52.6%
Avg.					11.50x		82.9%

バグ再現 (全 51 個)
- AFLGo : 34
- BEACON : 51

高速化
- 最低: 1.2x
- 最高: 68.5x
- 平均: 11.50x

枝刈り
- ほとんどの場合で
  80%以上枝刈り

実験 2: 事前条件による枝刈りと Reachability 解析による枝刈りの効果 #

BEACON では 2 つの枝刈りを行っている:

各変数の事前条件のによる枝刈り
Reachability 解析による枝刈り (Path Slicing)

実験設定:

	Path Slicing	事前条件での枝刈り	Relationship Preservation	Bounded Disjunction
BEACON	✅	✅	✅	✅
BEACON*	✅	❌	-	-

結果:

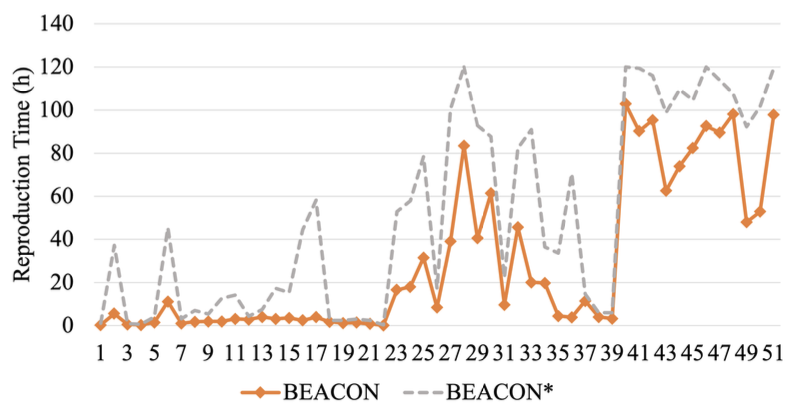
見方
- 横軸: 51 個の CVE
- 縦軸: バグの再現にかかった時間 (h)
BEACON* → 再現できないバグ有
- Time Out (>120h)
BEACON の方が速く再現できる
- 1.1x ~ 18.4x 速い

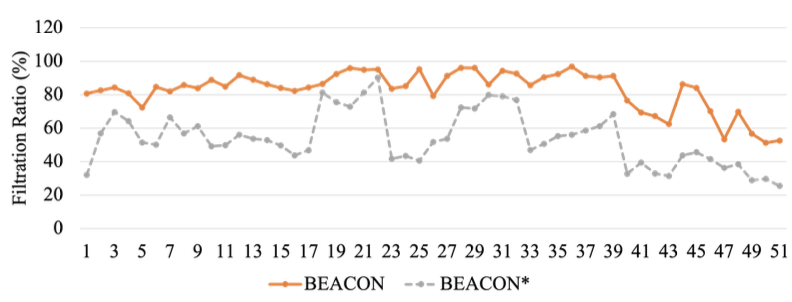
見方
- 横軸: 51 個の CVE
- 縦軸: 枝刈りできたパスの割合
事前条件による枝刈り
- 平均で 29.1% 多く枝刈りできる

→ 事前条件での枝刈りは fuzzing の効率化に貢献

実験 3: 抽象解釈における 2 つの最適化それぞれの効果 #

(事前条件を求めるための) 抽象解釈における最適化:

Relationship Preservation
Bounded Disjunction

実験設定:

	Path Slicing	事前条件での枝刈り	Relationship Preservation	Bounded Disjunction
BEACON	✅	✅	✅	✅
BEACON*	✅	❌	-	-
BEACON- $rp$	✅	✅	✅	❌
BEACON- $bd$	✅	✅	❌	✅

結果:

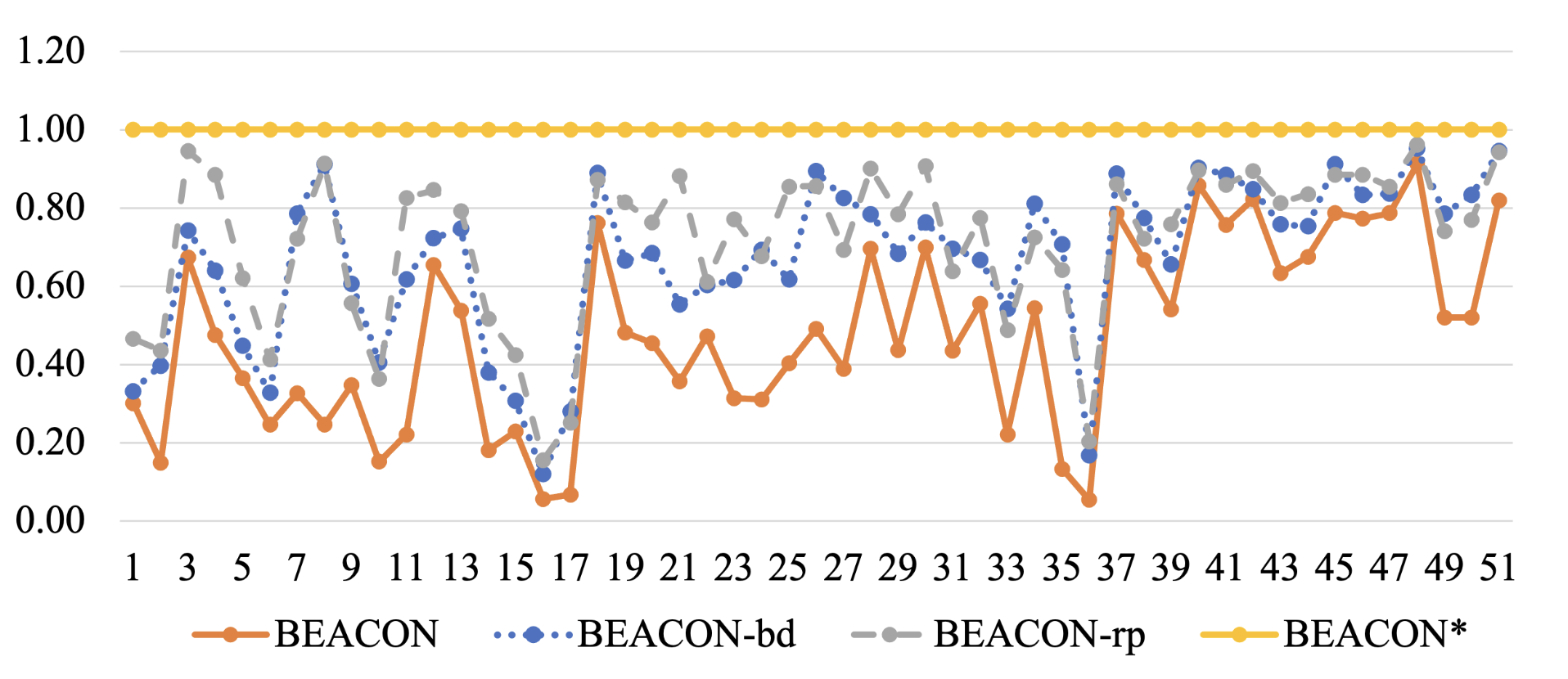
読み方
- 横軸: 51 個の CVE
- 縦軸: BEACON* に対するバグ再現までの時間の割合
観察
- BEACON- $rp$ → BEACON : 1.05x ~ 4.9x 速い
- BEACON- $bd$ → BEACON : 1.05x ~ 5.34x 速い
2 つの最適化が静的解析の精度向上に貢献している
- 枝刈りの精度向上 → fuzzing の効率化

実験 4: Fuzzing 時のオーバーヘッド #

$N_exec$ : プログラムの実行回数
$T_{orig}$ : 計装無しの実行時間
$T_{Beacon}$ : 計装有りの実行時間 (比較のため、枝刈りはせず条件比較のみ)

Project	$N_{exec}$	$T_{orig}$	$T_{Beacon}$	Overhead
Ming	126K	4.52m	4.80m	6.2%
Binutils	2.38M	2.48h	2.51h	1.2%
Libxml	25K	0.63h	0.65h	3.2%
Lrzip	1.07M	1.43h	1.57h	9.8%
Libjpeg	2.97M	0.59h	0.61h	3.4%
Libpng	1.41M	7.55h	8.01h	6.1%
Libpoppler	1.21M	23.73h	25.27h	6.5%
Libav	7.62M	23.87h	26.13h	9.5%

最大 9.8%, 平均 5.7%のオーバーヘッド
許容範囲内であるだろう

	入力	効率的か	オーバーヘッド	効率化のための工夫
AFLGo[CCS'17]	src+loc	❌	小	“距離” の導入
Hawkeye[CCS'18]	src+loc	❌	小	“距離” の計算方法の改善
FuZZGuard[SEC'20]	src+loc	❌	中(?)	機械学習ベースの手法、“良い"入力を学習させる
Savior[SP'20]	src	❌	大	1. ConcEx 2. 怪しい箇所の自動特定
BEACON[SP'22]	src+loc	✅	中	枝刈り

提案手法との関連 #

Transient Attack 関連の論文は以下に分類できる：

攻撃
Gadget 探索
CPU のテスト
防御
Transient Instruction の無効化
メモリ隔離 (memory isolation)
アーキテクチャレベルの隔離 (architectural isolation)
安全な投機実行 (secure speculative execution)
Covert Channel の無効化
時間的隔離 (time/temporal isolation)
その他
検証系

(学部) 提案手法: 動的テイント解析 + 動的キャッシュシミュレーター
- メモリアクセスに関する静的解析を行うことで、枝刈りを行える可能性
- その際の静的解析の参考になる
Gadget 探索:
- 「静的解析で得られた情報を基に枝刈り」というアイデアは活かせそう
- Directed-fuzzer は網羅的な Gadget 探索には向かない
  - が、fuzzing 効率化という面では役に立つ
    - e.g. 入力形式が複雑な場合に、正しい入力の発見を効率化

BEACON[SP'22] #

事前知識 #

概要 #

目標 #

課題 #

提案手法 #

結果 #

準備 #

区間抽象化による静的解析 #

Data-Flow Value (DFV) #

DFV の更新方法 #

DFV のマージ方法 #

具体例 #

定式化 #

区間抽象化における精度低下の原因 #

変数間の関係は追わないために精度が落ちる例 #

マージする時に精度が落ちる例 #

BEACON の手法 #

事前条件の計算 #

最適化 1. Relationship Preservation #

最適化 2. Bounded Disjunction #

DFV に対する変更 #

マージ方法に対する変更 #

事前条件に基づく計装 #

CFG 上での Reachability 解析 #

評価 #

実験 #

実験 1: 既存の fuzzing engine とのバグ再現における比較 #

実験 2: 事前条件による枝刈りと Reachability 解析による枝刈りの効果 #

実験 3: 抽象解釈における 2 つの最適化それぞれの効果 #

実験 4: Fuzzing 時のオーバーヘッド #

関連研究 #

提案手法との関連 #